Tutorial on Computational Fluid Dynamics (with python)
Date:
Introduction
In this course/tutorial, we use Python, a powerful and easy-to-learn programming language, to demonstrate the fundamental concepts of Computational Fluid Dynamics (CFD). Python has a rich ecosystem of libraries such as NumPy and Matplotlib which make it ideal for scientific computing tasks. In this notebook, we will solve a 2D heat convection problem using the finite difference method. The problem involves simulating the transport of heat in a fluid due to convection. This is a fundamental problem in fluid dynamics and heat transfer, with applications in many engineering fields.
Governing Equations
The governing equation for 2D heat convection is the 2D convection-diffusion equation, which can be written as:
\[\frac{\partial T}{\partial t} + u \frac{\partial T}{\partial x} + v \frac{\partial T}{\partial y} = \alpha \left(\frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2}\right)\]where:
- $T$ is the temperature,
- $t$ is the time,
- $x$ and $y$ are the spatial coordinates,
- $u$ and $v$ are the velocities in the $x$ and $y$ directions, respectively, and
- $\alpha$ is the thermal diffusivity.
This equation represents the balance of heat carried by the fluid flow (the convective term) and heat transferred due to temperature gradients (the diffusive term).
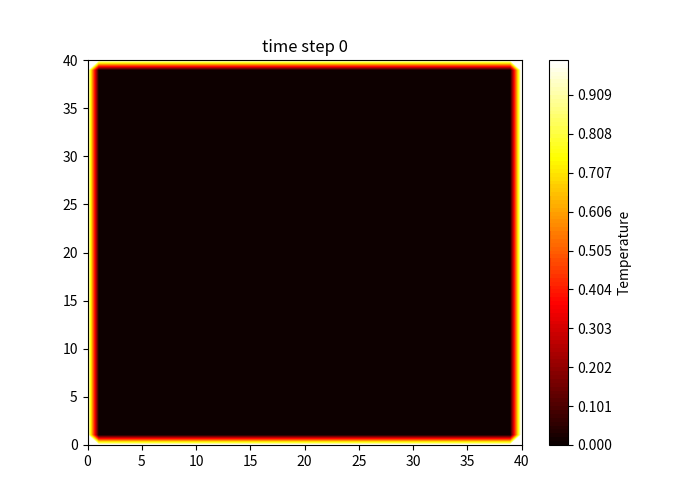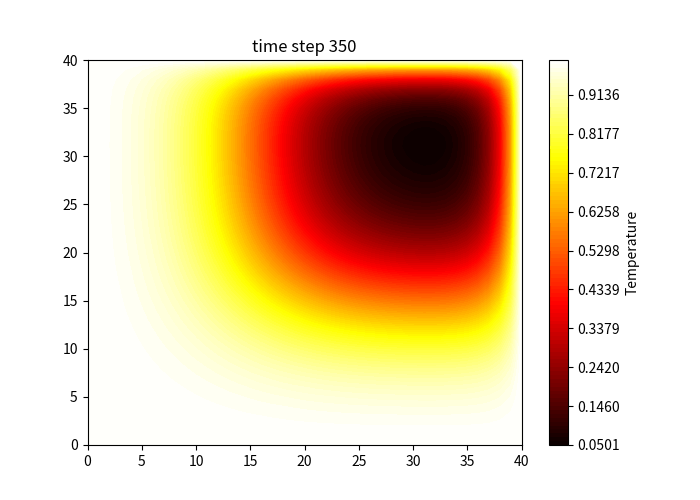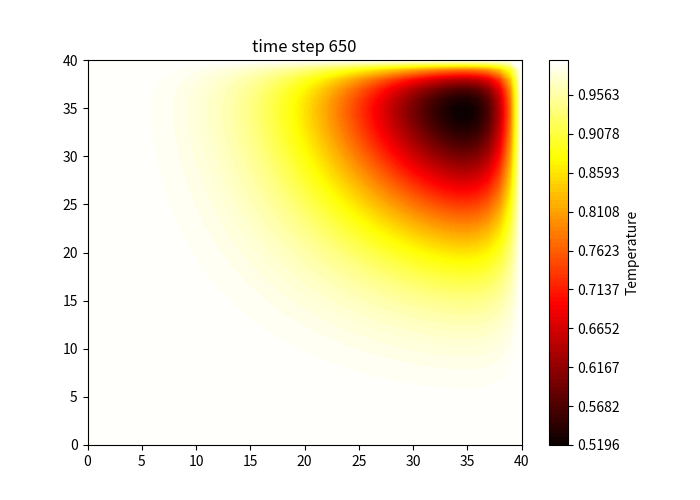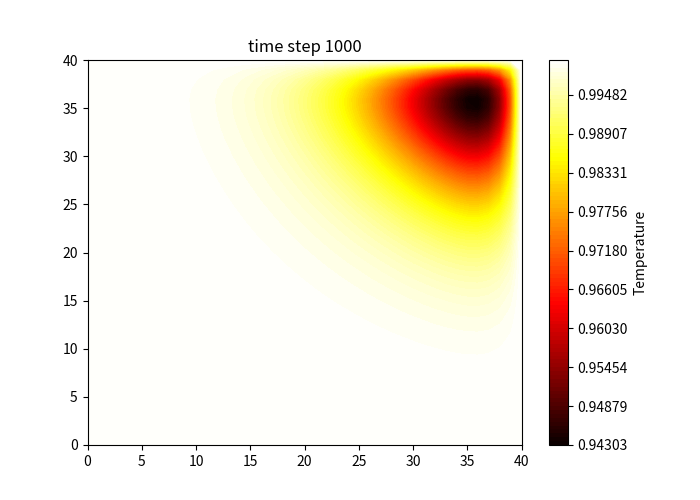
Result